IKF University of Frankfurt, GSI Darmstadt
The intensity and lifetime of low-charged ion beams in acceleration devices, such as synchrotrons or storage rings, critically depends on the charge exchange cross-sections for collisions with residual-gas atoms or molecules. In the present study, the charge-changing cross sections σtot and beam lifetimes t for stored many-electron ions, Mg1+, Ar2+, Pb29+, U4+, U10+ and U28+, and energies in the range of E = 1 - 100 MeV/u were calculated and compared with experimental data recently obtained at SIS/GSI [1, 2]. For the calculation, the following formulas have been applied:
σtot(v) = ΣTY(ZT)[σec(v) + σion(v)] (1) σion(v) = (ZT)2σp(v) + ZTσe(v) (2) τ(v) = [ρ ⋅ v ⋅ σtot(v)] -1, (3)
where v is the projectile velocity, σec is the one-electron capture cross section of the target electrons, σion is the single electron ionization cross section of the projectile, σp,e are proton- and electron-impact ionization cross sections, respectively, ZT is the nuclear charge of the target atom, ρ and Y(ZT) are the total density and the fractions of the residual gas atoms. The sum over T runs over all residual gas components. Note, that in contrast to highly charged heavy-ion beams, the low ionization potentials of low-charged projectiles give rise to large ionization cross-sections whereas electron capture into the fast moving ions can almost be neglected. In order to provide reliable cross-section estimates for ionization, the ionization potentials for all electron shells must be considered in the calculation. The latter, was performed in the framework of the non-relativistic Plane Wave Born approximation whereas the ionization potentials were taken from Ref. [3,4]. For completeness also electron capture into the projectile was taken into account by applying a semiempirical formula given in Ref. [5]. According to experimental and theoretical estimations of the rest gas conditions in the SIS/GSI [4], the following gas pressure and residual gas mixure were assumed:
ρ = (6.4 ± 1.3) ⋅ 10-11 mbar (4) Y(H2) = 77%, Y(N2) = 20%, Y(Ar) = 3%. (5)
Here, it is important to stress that in particular the uncertainty of the quoted Ar concentration is rather large. On the other hand, due to the (ZT)2-scaling of the loss-cross sections (see Eq. (2)), such high-Z components in the residual are of crucial importance for beam lifetime. In the figures, calculated values for total charge-exchange cross sections and lifetimes, Eqs. (1)-(5), are given and compared with experimental data. As can be seen in the figures, the theoretical estimates may differ by up to a factor of 2 to 3 from the experimental findings. This variance can be explained by the overall uncertainties introduced by i) the simplicity of the approximations used and ii) the uncertainty in the measured residual-gas pressure and its components (see [6] for details). To make more definite conclusions, future experiments are required where the gas pressure and the residual gas fractions are measured simultaneously with the beam lifetimes.
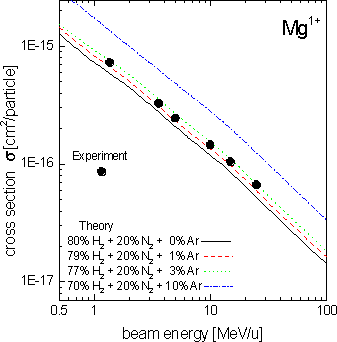
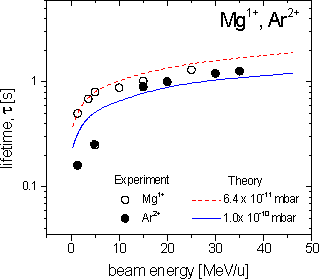
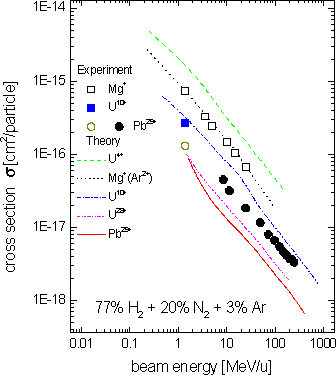
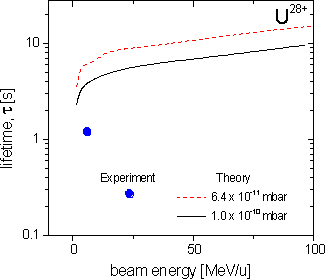
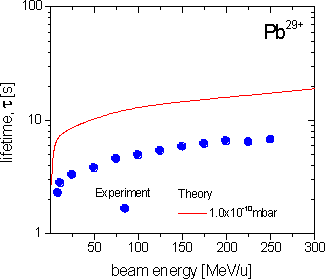
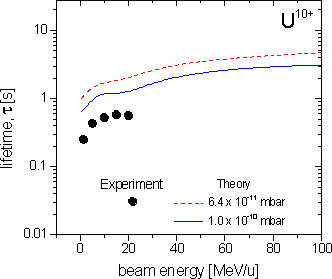
References [1] K. Blasche et al., GSI Scientific Report 1996, p. 159 (Darmstadt 1997). [2] P. Strehl, H. Reeg, D. Wilms, unpublished (SIS/GSI, Darmstadt 1997) . [3] T.A. Carlson et al., At. Data Nucl. Data Tables 2, 63 (1970). [4] K. Rashid et al., At. Data Nucl. Data Tables 40, 365 (1988). [5] A.S. Schlachter et al., Phys. Rev. A 27 , 3372 (1983) . [6] V.P. Shevelko, D. Böhne, Th. Stöhlker, Nucl. Instrum. Methods A 415, (1998) 609.
for further information,
please contact Thomas Stölker
Kai Lindenberg