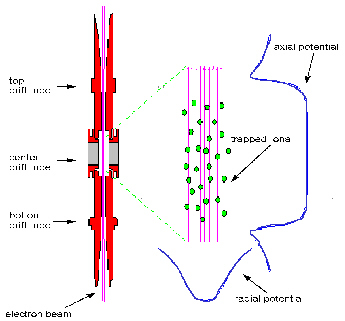
Figure 1: Schematic presentation of the operation principle of the Super-EBIT [4].
Besides the 1s binding energy in high-Z one-electron systems, the ground state of He-like high-Z ions gained increasing attention during recent years. Here, the two-electron contributions to the ground state energy can now be studied uniquely at traps for highly charged ions by measuring the radiative recombination (RR) transitions into the ground state of H-like ions relative to the one into the bare species [1,2 ]. This has been demonstrated in a first experiment conducted at the Super-Electron-Beam-Ion-Trap in Livermore, where RR transitions of free, fast moving electrons into the vacant 1s shell of bare and H-like ions has been exploited for precise spectroscopic studies. In particular, since the two-electron contributions are experimentally isolated, all one-electron contributions such as the effects of the finite nuclear size cancel out almost completely in this type of experiment [3].

Figure 1: Schematic presentation of the operation principle of the Super-EBIT [4].
A schematic presentation of the operation principle of Super-EBIT is depicted in Fig. 1 [4]. At Super-EBIT bare and H-like ions of almost any element can be produced in an electron beam of arbitrary energy up to 200 keV and currents up to 200 mA [5]. Here, the ions are injected into the trap either by a metal vapor vacuum source or by injection of neutral gas. Simultaneously to the production of the highly-charged ions by electron impact, the ions are trapped radially by the space charge potential of the electron beam. For the latter purpose also a magnetic field of three Tesla is applied, which in addition compresses the electron beam to a typical diameter of 50 mm. In the axial direction the trapping is achieved by electrostatic potentials applied to the end drift tubes of the EBIT device. Moreover, to avoid a too strong heating of the stored ions by the electron-ion collisions, evaporative cooling is applied in the trap by injection of neutral Ne gas. In contrast to a storage ring, in the S-EBIT the ions are stationary in the laboratory system and normally several charge states are confined simultaneously in the trap. With such collision conditions, the fast moving free electrons may undergo a direct radiative recombination transition into the vacant K-shell of the bare and H-like species. Since RR is the time reversal of the photoelectric effect, the energy carried away by the photon is just given by
![]() (4)
(4)
where Ekin denotes the kinetic energy of the electron captured and V is the ionization potential of the ionic system after undergoing radiative capture. Since both the bare and H-like ions are simultaneously trapped, i.e. both ion species are interacting with the same electron beam, the difference in the photon energies between radiative transitions into the bare and H-like ions is independent of the electron beam energy. It corresponds just to the difference in the ionization potentials between the H- and He-like species formed by the RR process which gives exactly the two-electron contribution to the ground state binding energy in He-like ions. A schematic presentation of this experimental situation at the EBIT is shown in Fig. 2. By applying the experimental method described above, data were obtained for Ge (Z=32), Xe (Z=54), Dy (Z=66), W (Z=74), Os (Z=76) and Bi (Z=83). For the experiments, x-ray spectra were taken by a solid state Ge(i) detector viewing the electron-beam/ion interaction zone through Be windows. They were saved in intervals of two hours in order to exclude the influence of possible electronic instabilities and drifts of the electron beam energy (for a detailed description of the data evaluation applied see Ref. [1]). In Fig. 3, sample spectra for the x-ray regime of RR into the vacant K-shell of germanium, xenon and bismuth are given separately. In all cases, the RR line splitting between RR into the bare and H-like ions appears well resolved.
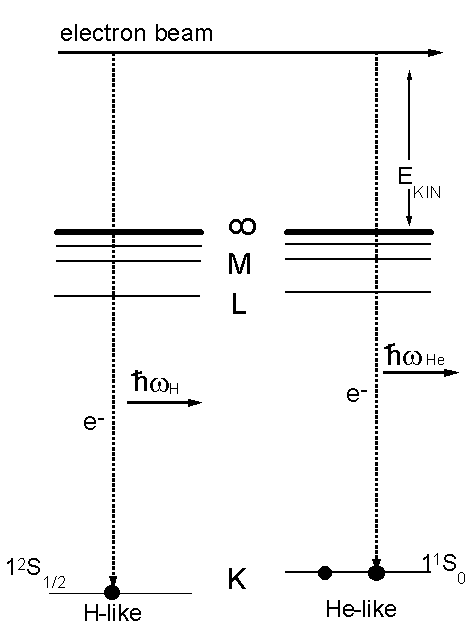
Figure 2: Schematic presentation of the RR process of free electrons into the initially bare and H-like ions. The energy difference h w H - h w He gives exactly the
two-electron contribution to the ionization potential in He-like ions.
Note that in contrast to fast ion-beam experiments the Doppler shift as well as the Doppler broadening are completely absent in this type of experiment. Here the width of the transition lines is almost completely determined by the intrinsic resolution of the Ge(i) detectors used. As observed in the spectra, the relative intensity of the peak from bare ions changes drastically between the two elements as the K-shell ionization cross section varies rapidly, as 1/Z4. Up to now, this has prevented the extension of the experiments to elements beyond Z=83.
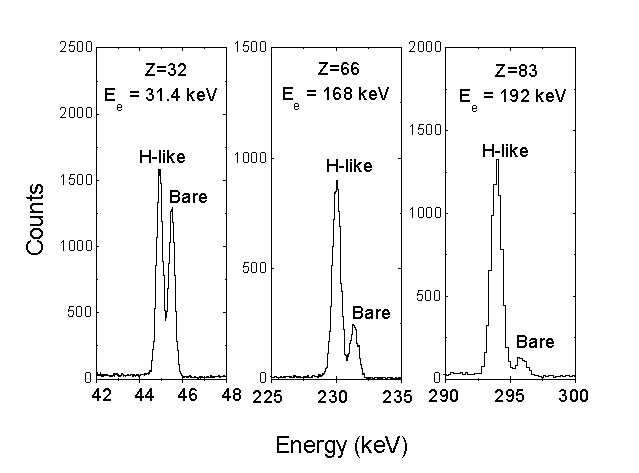
Figure 3: Sample K-shell RR line recorded for germanium (Z=32), dysprosium (Z=66), and bismuth (Z=83) at the Super-EBIT [1].
The experimental results obtained for the two-electron contributions to the binding energy of some He-like ions are given in Table 1 [1] in comparison with the theoretical calculations of Persson et al. [3] performed very recently. The experimental uncertainty quoted in the table is entirely determined by counting statistics. From the table an excellent agreement between experimental data and theoretical predictions can be seen. The predictions are based on relativistic many-body perturbation calculations (RMBPT) which take into account the non-QED part of the electron-electron interaction to all orders [3 ].
Table 1: The individual two-electron contributions to the ground state binding energy in some He-like ions [2 ] in comparison with the experimental results from Super-EBIT [1 ] (NR: non-radiative QED as defined by Persson et al. [3]; 2eVP: two-electron vacuum polarization; 2eSE: two-electron self energy; Total theory: predicted difference in the ionization potentials between the H- and the He-like system).
| Nuclear Charge |
1st order RMBPT(eV) |
2nd order RMBPT(eV) |
NR (eV) |
2eSE (eV) |
2eVP (eV) |
Total theory (eV) |
Experiment (eV) |
|---|---|---|---|---|---|---|---|
| 32 | 567.61 | - 5.20 | 0.0 | - 0.5 | 0.0 | 562.0 | 562.5± 1.6 |
| 54 | 1036.56 | - 7.01 | 0.2 | - 1.8 | 0.2 | 1028.2 | 1027.2± 3.5 |
| 66 | 1347.45 | -8.56 | 0.4 | - 3.2 | 0.6 | 1336.6 | 1341.6± 4.3 |
| 74 | 1586.93 | - 9.87 | 0.6 | - 4.6 | 0.9 | 1573.9 | 1568± 15 |
| 83 | 1897.56 | - 11.73 | 0.9 | -6.7 | 1.6 | 1881.5 | 1876± 14 |
In particular, the two-electron QED contributions are considered for the first time complete to second order in a . These include the non-radiative QED part as defined by Persson et al. [3] as well as the two-electron Lamb shift, i.e. the two-electron self energy and the two-electron vacuum polarization. Note, that compared to the QED calculations for high-Z H-like systems, where some higher-order QED effects are still uncalculated, the claimed theoretical uncertainty for the two-electron QED contributions is very small and, for the particular case of He-like uranium, estimated to be of the order of only 0.1 eV. Most importantly, as has been shown in detail by Persson et al. [3], the two-electron QED effects are almost completely unaffected by the uncertainties of the nuclear charge radius, one of the most serious limitations for the QED tests in high-Z one-electron systems. As can be deduced from the experimental and theoretical results presented in Table 4 the experimental data provide already a meaningful test of the many-body non-QED part of the electron-electron interaction. Moreover, the data are already at the threshold of a sensitive test of the two-electron QED contributions. For this purpose only a moderate increase in accuracy of about half an order of magnitude is required.
For the investigation of the ground state binding energy in He-like high-Z ions a novel technique has been introduced at the Super Electron Beam Ion Trap. The achieved experimental accuracy, which is only limited by counting statistics, already provides a meaningful test of the many-body part of the theory. In particular, only an improvement of half an order of magnitude is required for a test of the two-electron QED effects which, in contrast to the H-like systems, are almost unaffected by the finite nuclear size. For the latter purpose a more intense EBIT is required which is presently under construction and also the ESR storage ring seems to be well suited for such investigations in the future.
[1]R.E. Marrs, S.R. Elliott, and Th. Stöhlker, Phys. Rev. A52, 3577 (1995).
[2]Th. Stöhlker, S.R. Elliott, R.E. Marrs, Hyperfine Interactions 99, 217 (1996).
[3]H. Persson, S. Salomonson, P. Sunnergren, and I. Lindgren, Phys. Rev. Lett. 76, 204 (1996).
[4]R.E Marrs, Comments At. Mol. Phys., Vol. 27 No. 2, 57 (1991).
[5] R.E. Marrs, S.R. Elliott, D. Knapp, Phys. Rev. Lett. 72, 4082 (1994).
[6] R.E. Marrs, private communication (1996).